Weighted average return
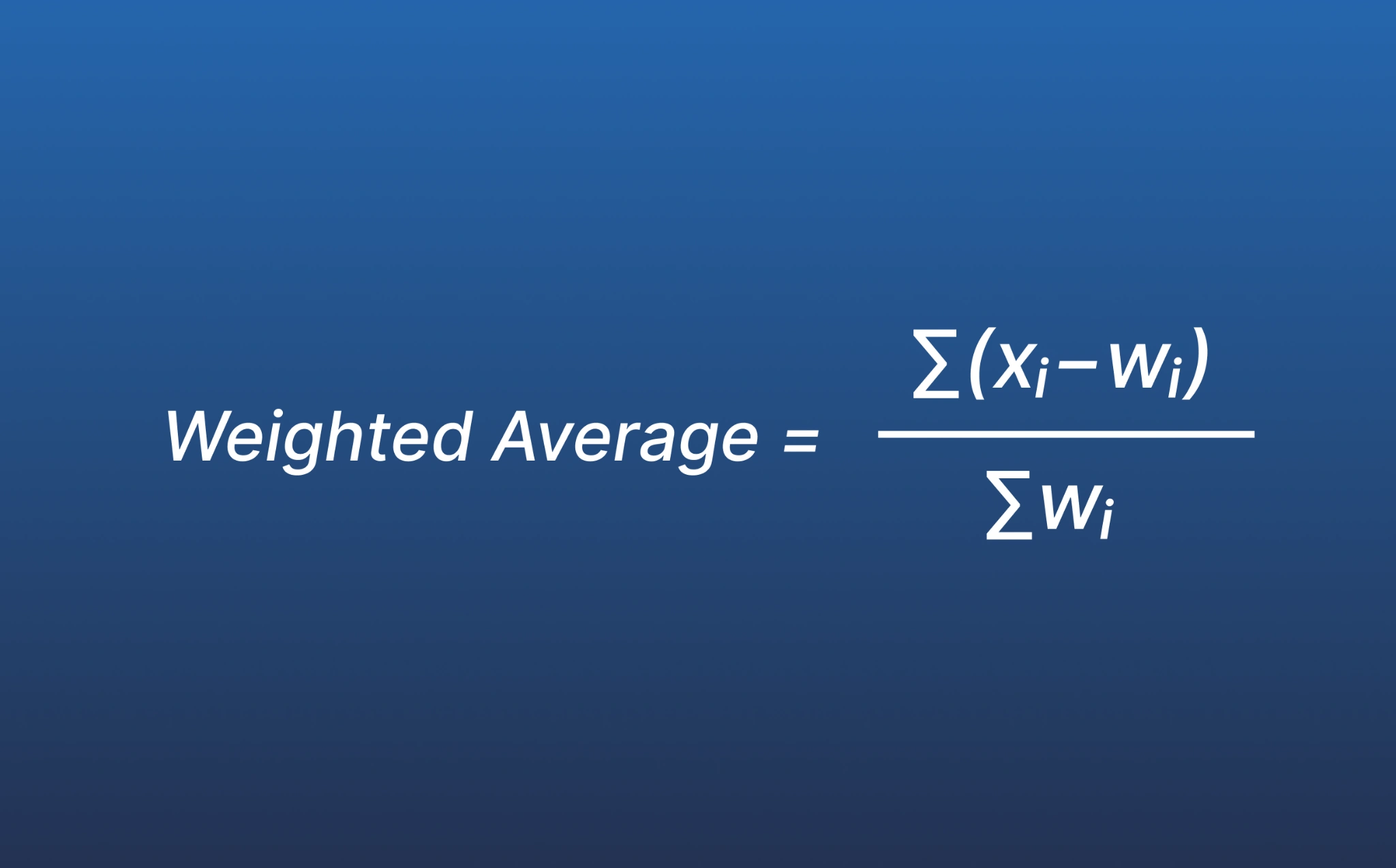
A weighted average is a statistical method that accounts for the varying importance or frequency of values within a dataset.
Unlike a simple average, which treats all values equally, a weighted average gives more influence to certain data points based on their significance. This makes it particularly useful when analyzing investments, financial performance, and datasets where some values carry more weight than others.
Weighted averages are widely used in investing, finance, statistics, and other fields where data points contribute differently to the overall result. For example, in a portfolio, larger investments have a greater impact on the total return than smaller ones. Understanding how to calculate and apply weighted averages can help make more informed financial decisions.
Planning calculations
Identify data components:
Start by listing the values and their weights, e.g. asset returns and their proportions.
Ensure weights total 100%:
Confirm that all weights add up to 100% (or 1). This is crucial for producing accurate results.
Choose the right format:
Use consistent units (like % or decimals) to avoid skewed results
Interpreting results
Interpret with context:
Weighted averages highlight key data. Focus on what the result means in real terms.
Increase savings when possible:
If values or weights change, recalculate to reflect the new situation.
Keep funds in the right place:
Use weighted averages to compare strategies, e.g. portfolios with different allocations.
1. What is a weighted average?
A weighted average is a calculation that assigns varying levels of importance to numbers in a dataset. It is particularly useful when certain data points are more significant than others.
This method is widely used in fields like finance, investing, and data analysis to provide a clearer picture of the dataset's true characteristics.
2. What is the purpose of a weighted average?
In investing, weighted averages are essential for accurately analyzing data when different assets or factors carry varying levels of importance. They ensure that the relative significance of each data point is reflected in calculations. Key examples include:
- Portfolio returns: - When calculating the overall return of an investment portfolio, more weight is given to larger holdings. For instance, if 70% of your portfolio is in stocks with a 10% return and 30% is in bonds with a 5% return, the weighted average return accounts for these proportions, providing a realistic measure of performance.
- Cost basis of shares: - Investors who buy shares at different prices over time use weighted averages to calculate the cost basis. For example, if 100 shares are purchased at $10 each and 50 shares are purchased at $40 each, the weighted average price accounts for both quantities and prices, yielding a clear picture of the average cost per share.
Weighted averages allow investors to evaluate their portfolios and costs more effectively, reflecting the true value of their investments rather than treating all components equally.
3. When to use weighted averages?
Weighted averages are particularly useful in scenarios where the values in a dataset have varying levels of importance or frequency. In investing, this method is commonly employed for more precise and meaningful calculations. Key examples include:
- Analyzing portfolio returns: - Use a weighted average to calculate the overall return of a portfolio where different asset classes (e.g., stocks, bonds, cash) have varying proportions and returns. This ensures the performance of larger holdings is accurately reflected in the total return.
- Calculating the cost basis of investments: - For investors who purchase shares at different prices over time, weighted averages are used to determine the average cost per share. This is essential for tax calculations and evaluating profitability.
- Comparing investment options: - When evaluating multiple investment opportunities, a weighted average can help compare the expected returns or risks of options based on their relative significance or weight in a portfolio.
Weighted averages are most effective when certain data points have a disproportionately large impact on the overall analysis, such as when larger investments dominate a portfolio or when specific factors carry more importance in decision-making.
4. Weighted average formula
Weighted averages are calculated using a formula that accounts for the value of each data point and its relative weight. This formula provides a more accurate representation of a dataset by prioritizing significant values.
Formula: The formula for calculating a weighted average is:
Weighted average =
Σ (xᵢ × wᵢ)
Σ wᵢ
Where:
xᵢ = Value of each data point
wᵢ = Weight assigned to each data point
Σ = Sum across all data points
Example
Consider an investment portfolio with three asset classes: stocks, bonds, and cash. The portfolio has the following allocations and returns:
- Stocks: 50% of the portfolio with a 10% return
- Bonds: 30% of the portfolio with a 5% return
- Cash: 20% of the portfolio with a 2% return
Therefore:
Weighted Average =
(10% × 50%) + (5% × 30%) + (2% × 20%)
100%
= 6.9%
Calculator
Try our calculator to calculate how much you might need to save each month to hit your goal. If you want more control,
try our stand alone weighted average return calculator.
5. Applications of weighted average
Weighted averages are widely used across various fields to provide more accurate and meaningful insights by accounting for the relative importance or frequency of data points. This approach ensures that the final results better reflect the underlying dynamics of the dataset. Below are some key areas where weighted averages play a critical role:
- Investing: - Weighted averages are essential for calculating the cost basis of shares bought at varying prices over time. They also help assess the overall return of a diversified investment portfolio by accounting for the proportional contributions of different asset classes.
- Finance: - A crucial tool in determining the Weighted Average Cost of Capital (WACC), weighted averages enable businesses to evaluate their overall cost of funding. This helps in making informed decisions about investments, mergers, and acquisitions.
- Statistics: - Weighted averages ensure that survey results accurately represent all groups, especially underrepresented ones. By adjusting for frequency or importance, they enhance the credibility and fairness of data analysis.
6. Advantages and disadvantages of weighted averages
Like any method, weighted averages come with both strengths and limitations. Understanding these can help you decide when this approach is most appropriate.
Advantages:
- Delivers a more accurate picture by factoring in the importance of each data point.
- Reduces the impact of outliers that might distort simple averages.
- Widely applicable. Useful in finance, research, engineering, and more.
Disadvantages:
- Assigning weights can be subjective and may introduce bias.
- Highly sensitive to data or weight changes, which can shift results significantly.
- Requires more effort and data compared to basic averaging methods.
7. Summary
Weighted averages provide a more accurate and nuanced approach to analyzing data where values carry varying levels of importance. By applying appropriate weights, this method ensures that datasets better reflect their true characteristics. It is extensively used across fields such as finance, investing, and statistics to deliver meaningful insights.
However, the reliability of weighted averages depends on the careful assignment of weights, as subjective or inaccurate weighting can introduce bias. Despite its complexity compared to simple averages, the weighted average remains a vital tool for precise and tailored data analysis.